Some chemical elements have isotopes that are inherently unstable and undergo radioactive decay. (Isotopes of the same element always have the same number of charged protons in each atomic nucleus, but have different numbers of noncharged neutrons. Isotopes of a single element act the same chemically, but often behave differently as regards radioactivity or other nuclear reactions.) Each radioactive isotope has a remarkably constant decay rate. These can be measured quite accurately, and most are constant under a huge range of conditions (temperature, pressure, and so on). The laws of physics do not tell us which atoms of a given isotope (say, uranium-238) will decay at any given time; but they do tell us how long it will take for, say, half of the atoms to decay — this duration is called the "half-life"; it is independent of the size of the sample. It is a lot like insurance mortality tables — for a given age group, actuaries cannot predict which individuals are good risks, but they can predict things such as the average life expectancy of members of the group and how long it will take for half of the group to succumb to accidents or natural causes.
"Simple" radioactive dating can be visualized as using a kind of atomic hourglass. The radioactive "parent" decays into a "daughter" isotope (often of a different element, since radioactive decays usually involve charged particles). So, if both parent and daughter elements are present, the ratio of parent isotope to daughter isotope can give a clue to the age of the sample. If there is more parent than daughter, the sample is still young (the top of the hourglass is still mostly full). If there is less parent than daughter, the sample is old (most of the sand is at the bottom of the hourglass).
But simple dating techniques can be distorted in several ways. What if there were some of the daughter isotope in the sample when it was formed? (Or, by analogy, what if the hourglass had some sand already in the bottom vessel when the hourglass was first placed upright?) What if the sample were not a "closed system", and isotopes (either parent or daughter) could enter or leave the system? (What if there were holes in either vessel of the hourglass that could let sand grains in or out?) Such contingencies clearly could affect estimates of how long the "clock" has been running.
To give a concrete example, suppose that we examine 3 different minerals from a rock, labeled A, B, and C, and that isotopic tests revealed the relative amounts of 3 chemical isotopes in these minerals. The parent isotope is rubidium-87 (87Rb for short). It is radioactive, has 37 protons and 50 neutrons (for a total of 87 nucleons), and beta-decays to strontium-87 with a half-life of 49 billion years. The daughter isotope, strontium-87 (87Sr), has 38 protons and 49 neutrons (for a total of 87 nucleons). 87Sr is formed when one neutron of a 87Rb atom decays to a proton, ejecting an electron (or "beta ray"). A third isotope required is strontium-86 (86Sr); this is not involved in any radioactive reactions (and thus is "non-radiogenic").
The present-day relative amounts of the isotopes in our fictitious example are:
| Mineral | 87Rb | 87Sr | 86Sr |
| A | 60 | 80 | 40 |
| B | 30 | 60 | 60 |
| C | 10 | 60 | 100 |
These numbers are purely hypothetical — they were chosen so the explanation would be easy to understand. I decided to make the rock 49 billion years old, one half-life of rubidium. (Yes, that is much older than the universe, but this is merely an example.)
If we were to apply the "simple" dating method to A, B, and C, we would arrive at 3 different ages, assuming that there was no initial daughter isotope (87Sr) when the rock formed. For mineral A, all 80 units of 87Sr would be assumed to have once been 87Rb, so the initial amount of 87Rb would be 60 + 80 = 140. The corresponding age works out to be 1.222 half-lives, or about 60 billion years. [T = T1/2 log2((87Rb + 87Sr) / 87Rb) = 49 BY log2(140 / 60)]. Similarly, mineral B would appear to have an age of 78 BY, and mineral C would appear to have an age of 138 BY. Thus the presence of initial daughter atoms devastates the validity of "simple" dating methods.
There are 3 important questions to consider when choosing a mineral sample for radiometric dating: (1) Is the rock a good sample for radioactive dating? (2) What was the initial amount of daughter product (87Sr) in the rock at the time it formed out of a melt? (3) How old is the rock? The isochron technique provides a way to answer these questions.
Imagine going back in time 49 billion years to observe the rock as it is crystallizing from a melt. The rock has both isotopes of strontium: the daughter product 87Sr and non-radiogenic 86Sr. Because these all have nearly identical chemical characteristics, they are mixed in equal ratios throughout the melted rock, much as a drop of food coloring stirred into a glass of water quickly diffuses into a uniform hue. Ratios are the "secret" of the isochron method, and we need just 2 ratios: the ratio of the radioactive parent isotope (87Rb) to the non-radiogenic isotope (86Sr), and the ratio of the daughter isotope (87Rb) to the same non-radiogenic isotope (86Sr). These are given in the following table for the assumed time of crystallization (49 BY ago).
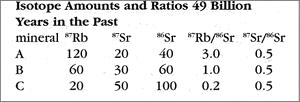
The rubidium-heavy mineral A has the highest ratio; A’s ratio of parent isotope to non-radiogenic isotope is 120 / 40 = 3.0. In contrast, the rubidium-poor mineral C has the lowest ratio; C’s ratio of parent isotope to non-radiogenic isotope is 20 / 100 = 0.2. Note that all of the minerals have the same ratio of daughter isotope to non-radiogenic isotope: 0.5, or 1/2. This is a direct result of the uniform mixing of the melted isotopes.
Now let us return to the present and see what has happened to our rock. The next table shows the present-day amounts and ratios of the isotopes.
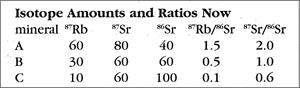
Because the time elapsed since the rock solidified is one half-life of 87Rb, half of the ancient amount will have decayed by the present. So for mineral A, which started with 120 units of 87Rb, now 60 remain, with the other 60 converted to the daughter isotope (87Sr). Thus, as the 87Rb amount drops from 120 to 60, the 87Sr count goes from 20 (49 BYa) to 80 (now). The story is similar for mineral B, which has an 87Rb change of 60 down to 30, and a corresponding 87Sr increase of 30 up to 60. Try the rule out on mineral C to see for yourself how this works. The important thing is that the ratios have changed also — the 87Rb ratios all dropped, and the 87Sr ratios, which used to all be 1/2, are now quite different (ranging from 0.6 to 2.0).
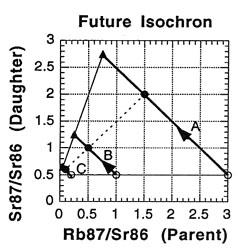
So what is an isochron, anyway? If the results of the preceding tables are graphed with the parent isotope ratio as the horizontal axis, and the daughter isotope ratio as the vertical axis, then the slope of the isochron — the line connecting the points for the various minerals at the same time (as the etymology of the name "isochron" suggests) — is directly related to the age of the rock. Two such isochrons are shown below: the horizontal one labeled 49 BYa, and the slanted one (lower left to upper right) labeled NOW.
The lines with arrows represent the changes in those single minerals over time. For example, A’s 87Rb/86Sr ratio drops from 3.0 to 1.5, while its 87Sr/86Sr ratio rises from 0.5 to 2.0. Compare the plot to the ratios in the preceding tables to see where the isochrons come from.
How is the isochron’s slope related to the age of the rock? Let us consider one more example — that of the same rock, 49 BY in the future (long after our sun has turned into a smoldering dwarf star).
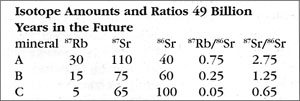
The slope of the far-future isochron is (2.75 - 0.65) / (0.75 - 0.05) = 2.1 / 0.7 = 3.0. The age is obtained by adding 1.0 to the slope, and then stating the sum as a power of two; that power is the age, in half-lives. For a slope of 3, 3 + 1 = 4 = 22, so the age is 2 half-lives. For a slope of 1 (present-day), 1 + 1 = 2 = 21, so the age is 1 half-life. And for a slope of 0.0 (49 BY ago), 0 + 1 = 1 = 20, so the age is zero. In general, the number of half-lives is the base 2 logarithm of (the isochron’s slope + 1). For a slope of 7, slope + 1 = 8 = 23, which means 3 half-lives.
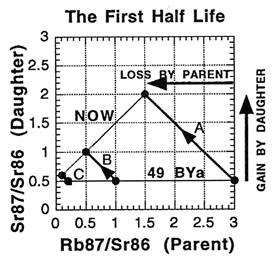
When applied correctly, the isochron method provides a powerful way to tackle some of the problems encountered with "simple" dating techniques. For one thing, if the sample minerals did not solidify at the same time but were mashed together, the points will generally not lie on a straight line. And when this scattering is observed, the sample is recognized to be unusable for dating with the method. It is like a built-in quality check on the reliability of the result. For another thing, the possibility of having some of the daughter isotope already present in the rock when it formed can be handled . This initial amount is revealed by the isochron method — as the value on the 87Sr/86Sr axis where the isochron crosses (0.5 in all the examples). And since the age depends on the isochron slope, the initial amount does not affect the age determination (unlike "simple" dating).
But the method is not infallible. For example cases of non-uniform mixing, or conglomeration of certain types of rocks, can sometimes lead to "false" or "fictitious" isochrons — isochrons that do not represent the true age of the rock. These possible pitfalls are discussed in Bernard-Griffiths (1989) and Faure (1986). There are methods to counteract these problems, such as taking more mineral samples, performing mixture analyses on more than one element, and by checking dates by independent means (such as looking at different parent/daughter pairs). (For more details on this and other methods, see the chapter on dating techniques in Dalrymple [1991] and York and Dalrymple [2000].) When such checks are made, confidence in the results is greatly increased. For example, the St Severin meteorite was dated with three different methods (Rb-Sr, Sm-Nd, and Ar-Ar) as being between 4.4 and 4.6 billion years old (Dalrymple 1991, 288).
Creationists love to attack such methods by claiming that we do not really know if radioactive decay rates are constant over time. They point out no human was around back then, so who knows for sure? They also hypothesize that decay rates varied during supernatural events (the Creation, the Flood), but of course they do not test these hypotheses. One interesting point against the creationists is the fact that, if decay rates did change over time, the points on an isochron plot would be forced off the isochron line and would appear quite scattered. The very fact that isochrons do work in many cases is powerful evidence that decay rates have, in fact, remained constant for billions of years.
This article originally appeared in NMSR Reports 1997 May; 3 (5): 5–7. It is reprinted and abridged with permission.
